- Услуги
- Цена и срок
- О компании
- Контакты
- Способы оплаты
- Гарантии
- Отзывы
- Вакансии
- Блог
- Справочник
- Заказать консультацию
Заказать консультацию
Дельта-гамма-вега-приближение
Если в портфеле содержатся опционы, то применение к нему дельта-нормального подхода для расчета VaR сталкивается со следующими проблемами:
- дельта портфеля может изменяться очень быстро (высокая гамма);
- дельта портфеля может быть различной для роста и падения цены базисного актива;
- возможна ситуация, когда предельные потери по инструменту нельзя оценить исходя из предельных отклонений цены базисного актива в обе стороны, т. е. функция изменения стоимости является немонотонной. В этом случае следует проверять поведение стоимости портфеля во всех промежуточных состояниях базисного актива.
Один из главных недостатков дельта-нормального подхода заключается в том, что он не учитывает какие-либо иные виды риска, кроме риска дельты. Однако в рамках данного подхода в расчет могут быть также включены и показатели, отражающие гамма- и вега-риск, которые представляют собой ряд Тейлора, аппроксимирующего приращение функции стоимости инструмента V: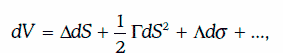
где Δ, Г, Λ – оценки дельты, гаммы и веги соответственно для портфеля в целом;
S – цена базисного актива.
Дельта-гамма-вега-приближение (delta-gamma-vega approximation) позволяет рассчитывать VaR для портфеля опционов с одним и тем же базовым активом по следующей формуле (1):
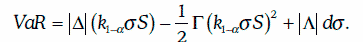
Если гамма отрицательна, что соответствует короткой чистой позиции по портфелю опционов, то второе слагаемое в формуле (1) увеличит риск, в то время как положительная гамма скорректирует величину VaR в сторону снижения.
Если чистая позиция по опционам оказывается длинной (т. е. имеет положительную вегу), то риск портфеля будет возрастать при снижении волатильности базисного актива. Напротив, при короткой чистой позиции (т. е. отрицательной веге) риск портфеля будет увеличиваться при росте его волатильности.
Хотя дельта-гамма-вега-приближение учитывает нелинейные характеристики риска, остаются следующие проблемы:
- в методе предполагается нормальное распределение как доходностей базисных активов (факторов риска), так и их квадратов, что, как правило, не выполняется ни в теории, ни на практике;
- объем вычислений возрастает геометрически с ростом числа факторов риска. Так, при использовании только дельта-гамма-приближения уже при 100 факторах риска требуется рассчитать 100 оценок дельты, 5050 значений элементов ковариационной матрицы и дополнительно 5050 элементов матрицы коэффициентов гамма, включающей вторые частные производные по каждой позиции портфеля по каждому фактору риска;
- необходимость проверки поведения стоимости портфеля при всех промежуточных состояниях факторов риска сохраняется, если он состоит из нелинейных инструментов с немонотонной функцией изменения стоимости.
Важно также иметь в виду, что в случае, когда доля опционов в портфеле существенна, волатильность портфеля за период не пропорциональна квадратному корню из отношения временных горизонтов, и ее следует оценивать непосредственно для интересующего временного горизонта расчета VaR путем полного оценивания.
Для больших диверсифицированных портфелей, в которых опционы не доминируют, дельта-нормальный метод представляет собой наиболее быстрый и эффективный способ расчета VaR. Для портфелей, чувствительных к относительно небольшому количеству источников риска с некоторой (существенной) долей опционов, дельта-гамма-вега-приближение обеспечивает более высокую точность при сравнительно невысоких требованиях к вычислительной мощности. Для портфелей со значительной долей опционов необходим подход на основе полного оценивания, который предусматривает полную переоценку портфеля при различных значениях базисного актива и иных факторов риска:
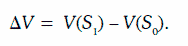
Статьи по теме
- Краткий обзор Нового базельского соглашения по капиталу
- Модель управления активами и пассивами (ALM)
- Метод сигналов
- Подход на основе регрессионного анализа
- Модели возникновения финансовых кризисов
- Минимальные требования к достаточности капитала с учетом кредитного и рыночного рисков
- Подход на основе внутренних моделей банков. Верификация моделей расчета VaR по историческим данным
- Подход на основе внутренних моделей банков. Количественные критерии
- Подход на основе внутренних моделей банков. Качественные критерии
Полезные статьи









Узнайте цену услуг:
Узнай цену консультации
"Да забей ты на эти
дипломы и экзамены!”
(дворник Кузьмич)

